今回は”才能を数学的にどう記述するか”をメインに記事にしました。
才能を曲線で表したらどうなるか 、才能がないとは数学的にどう定義できるのかを書きました。よかったら続きをご覧ください。

成長を表す数学的モデル
このまま勉強を続けても無駄だって思ったことはありませんか?勉強しても全く効果が出ないと嘆いている人はたくさんいると思います。成長していないと感じていても、実は成長していると言うことを数学で証明していきます。

必要知識
- 微分(数2)
- 接線の傾き(数2)
成長曲線の種類
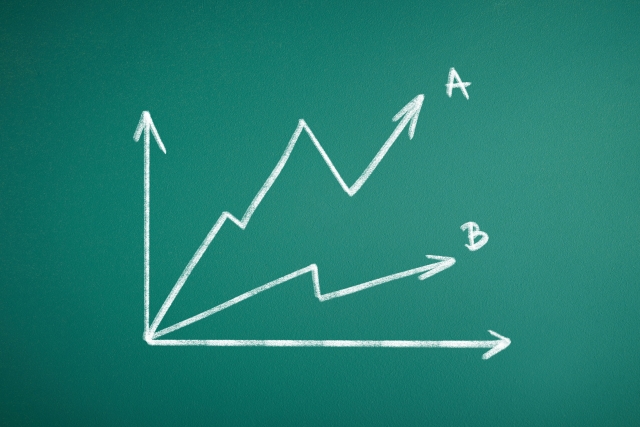
まずは成長曲線というものを定義したいと思います。x軸を努力量、y軸を結果スコアとしてグラフを見てください。
その1:素晴らしい成長曲線
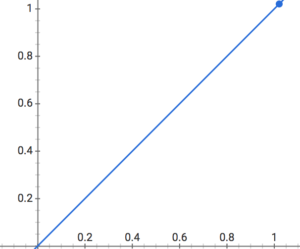
まずは努力すれば努力するほどそれに比例して成長していく人の成長曲線です。天才と呼ばれる人にはいくつかのタイプがあって、やればやるほどぐんぐん伸びる人も天才と言われますよね。
最初から抜群に出来る人も天才と呼ばれますが、この場合はy切片が高い位置にあると考えれば表現できます。つまり、この場合の才能というのは数学的に言えば、成長曲線で表現できるということです。
その2:ちょっと微妙な成長曲線
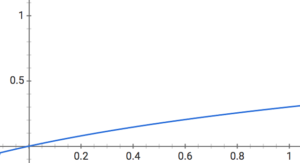
同じ努力をしてもその成果は人によって違います。100の努力をしても50しか得られない人だっています。そういう人の成長曲線を簡単に表してみました。
でもグラフのように各段階で成長していると感じられれば御の字でしょう。
その3:まるで成長しない曲線
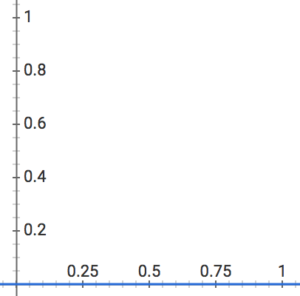
どれだけ努力しても全く成長しないという人もいます。私も、英語をどれだけ勉強してもこの成長曲線のように、全く伸びた感じがしません。
このグラフはどれだけ努力しても成長しないということを表していますが、ある特定の期間だけ成長しない人も中には居ますよね。
もっと難しい話をすると”ある1点成長しない”ということも理論的には考えられるわけです。”成長しない”の定義を数学的にしてみましょう。
成長しないの定義
努力量を\(x\)として、点\(x\)で成長していないということは、成長曲線のそこでの微分係数が\(0\)であると定義しましょう。簡単に言えば、その点での曲線の傾きが0ということです。
微分係数の意味
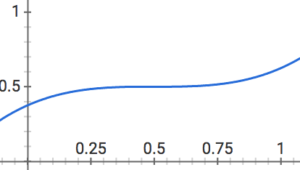
例えば上の成長曲線では、\(x=0.5\)で成長していません。他の全ての点ではギリギリ成長しています。ちなみにこの成長曲線のモデルは\(y=(x-0.5)^3+0.5\)です。
成長を感じるときは微分係数が正で、成長を感じないときは微分係数が\(0\)であると考えるのはすごく自然に思えます。
ほとんど確実に成長しない
”全く成長しない”というのは"!全ての点で微分係数が0"ということにしましょう。この場合、微分をして常に"\(0\)"な関数は定数関数以外にありませんから、努力をしても本当に成長しないことになります。
次に、”ほとんど確実に成長しない”ということの定義をしましょう。
”ほとんど確実に成長しない”というのを"努力をしても成長しない確率が\(1\)"と定義することにしましょう。つまり、"微分係数が0である確率が\(1\)"ということです。具体例は次の図です。

このグラフでは真ん中の1点を除いて成長していません。無限にある点から真ん中の点を選ぶ確率は"0"なので、成長していない確率は"1"になります。よってこの場合はほとんど確実に成長していません。
大学数学をノゾキ見
"ほとんど確実に"というのは実はちゃんとした数学用語で、大学数学の測度論・確率論で姿を表します。
例えば\(0\)から\(1\)の間の実数を選んだ時にそれが有理数である確率は"0"なので、\(0\)から\(1\)の間の実数から数字を選んだとき、ほとんど確実にその数字は無理数であると言えるということです。
悪魔の階段
先程あげた例では、成長曲線が不連続であるがために一瞬で一気に成長してしまう時期があります。ですが現実にはそういったことは起こりえないと思います。
認識するのは成長した後だとしても、成長自体は連続的に起こっているということです。
そこで質問です。ほとんど確実に成長はしないけど成長自体は起こっていて、しかもその成長は連続的である場合ってあると思いますか?つまり数学的には次を満たす関数があるかどうかです。
次を満たす関数\(f(x)\)はあるか?
- \(f'(x)=0\)である確率が\(1\)
- 関数\(f(x)\)は\([0,1]\)上で連続
- \(f(0)=0\)かつ\(f(1)=1\)を満たす
言い換えれば"微分がほとんど\(0\)で連続なのに最初と最後の値が違う関数"です。
微分がほぼ\(0\)であるだけならさっきの階段のような関数が作れますが、連続という条件がつくと、どこかの点で値が増えていないと\(f(0)=0,f(1)=1\)なんてなりませんよね。

しかし、関数の値が増えていたとするとその点で微分が\(0\)ではなくなるわけです。そうなるとそんな曲線は存在してはいけないかのように思いますよね?
でも実は存在します。ほぼどの点を取っても微分が\(0\)で全ての点で連続で、しかもいつの間にか増加している関数が存在します。"悪魔の階段"と呼ばれる関数です。

ほんとど確実に成長しない連続関数
悪魔の階段の形は複雑すぎて正確なグラフではかけませんが、概ね次のような形をしています。
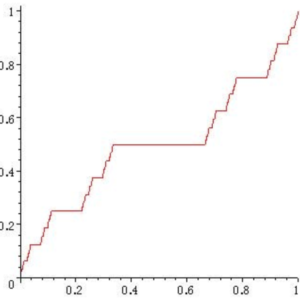
悪魔の階段の導入まで長くなりましたが、話を戻させてもらえば、私たちの成長というのはこの悪魔の階段だと私は言いたいのです。常に成長していないと感じるのに、実は連続的に成長していってるということです。
まとめ
ずっと平坦な道を歩いてきたのにいつの間にか富士山の頂上にいた。成長とはそういうものです。これが数学的に起こり得ることを悪魔の階段は教えてくれます。
階段はないはずなのに気づいたら階段を登っていた、その怖さを揶揄して悪魔の階段と呼ばれています。